Learning Objectives
By the end of this lab session, you should be able to:
- Use Greedy Algorithm to solve 3 classic academic problems.
- Appreciate the intuitive simplicity and effectiveness of Greedy Algorithm.
- Understand that Greedy algorithms do not always yield optimal solutions, but for many problems they do.
Overview of Lab Activities
Here are the activities for which you will upload solutions to xSITe or Gradescope:
Exercise 1: Gas Stops
You are driving a car from city A to city B. The distance between the two cities is D miles. Your car can travel up to M miles on a full tank of gas. Along the way, there are N gas stations at distances S1,S2,…,SN miles from city A (with S1 < S2 < ⋯ < SN < D) You start with a full tank of gas.
Your task is to determine the minimum number of stops you need to make to reach city B. If it is not possible to reach city B, return −1.
Input
- An integer D representing the total distance to the destination.
- An integer M representing the maximum distance the car can travel on a full tank.
- An array S of length N, where S[i] is the distance of the i-th gas station from city A.
Example Input
- Enter the total distance (D): 25
- Enter the maximum fuel range (M): 10
- Enter the distances of the gas stations separated by spaces: 10 14 20 21
Output
- The minimum number of refueling stops required to reach city B, or −1 if the destination is not reachable.
Example Output
- Minimum number of stops: 2
- Destination is not reachable.
Template: Gas Stops
You can find the template files on GitHub repository. Complete the partial gas_station.cpp file. The make command will compile the project.
To receive credit for your work, upload your completed gas_station.cpp file to the Gradescope assignment titled [“Gas Stops”]
Hints: Gas Stops
- Initialize: Set your current position to city A and your fuel level to M.
- Iterate Through Stations:
- For each gas station, check if it’s within your current fuel range.
- If yes, move to that station and update your fuel level.
- If no, refuel at the previous station (the farthest one you could reach) and increment your stop count.
- Refuel will be to full tank.
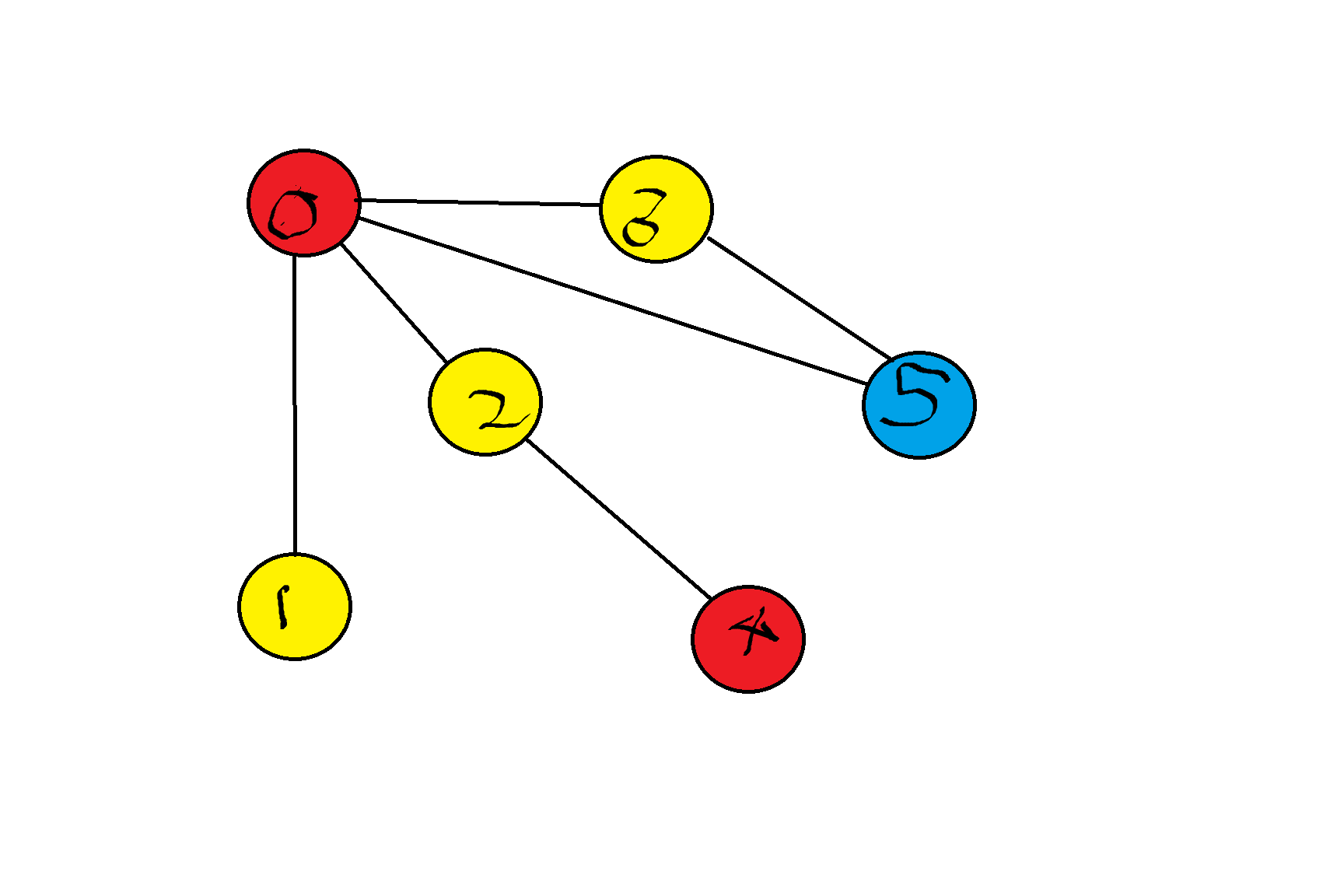
Exercise 2: Color Graph
You are given an undirected graph represented by n vertices and m edges. Write a program to determine the minimum number of colors required to color the graph such that no two adjacent vertices have the same color.
Input
- Number of edges
- Each edge as two space-separated integers
Example Input
- Enter the number of edges: 6
- Enter each edge as two space-separated integers (e.g., ‘0 1’):
0 1
0 2
1 2
1 3
2 4
3 4Output
- Print the color assigned to each vertex and the total number of colors used.
Example Output
Vertex Color
0 0
1 1
2 2
3 0
4 1
Minimum number of colors required: 3Template: Color Graph
You can find the template files on GitHub repository. Complete the partial graph_coloring.cpp file. The make command will compile the project.
To receive credit for your work, upload your completed graph_coloring.cpp file to the Gradescope assignment titled [“Color Graph”]
Hints: Color Graph
This problem is NP-complete, meaning that finding an exact solution efficiently for large graphs is computationally infeasible.
However, heuristic approaches like the greedy coloring algorithm can provide approximate solutions. The greedy algorithm doesn’t always yield the optimal (minimum) number of colors. Its effectiveness heavily depends on the vertex ordering.
Ref TextBook Section 34-3 for more graph coloring problems.
Exercise 3: Knapsack
You are a backpacker and you have a knapsack with a weight capacity of W. You are given n items, where each item has a weight and a value. Unlike the 0/1 knapsack problem, you are allowed to take fractions of items (i.e., you can take a part of an item, not necessarily the entire item).
Your goal is to maximize the total value of the items in the knapsack without exceeding the weight limit.
Input
- n (1 ≤ n ≤ 1000): The number of items.
- W (1 ≤ W ≤ 10^4): The weight capacity of the knapsack.
- An array of n elements where each element represents an item, containing:
- weight[i] (1 ≤ weight[i] ≤ 10^4): The weight of the i-th item.
- value[i] (1 ≤ value[i] ≤ 10^4): The value of the i-th item.
Example Input
- Enter n the number of items: 3
- Enter W the weight capacity of the knapsack: 50
- Enter the elements of the array where each element represents an item’s weight: 10, 20, 30
- Enter the elements of the array where each element represents an item’s value: 60, 100, 120
Output
- The maximum value that can be carried in the knapsack, up to two decimal places.
Example Output
- Maximum value that can be carried: 240.00
Template: Knapsack
You can find the template files on GitHub repository. Complete the partial knapsack.cpp file. The make command will compile the project.
To receive credit for your work, upload your completed knapsack.cpp file to the Gradescope assignment titled [“Knapsack”]
Hints: Knapsack
Calculate Value-to-Weight Ratio: For each item, compute the ratio of its value to its weight (value/weight).
Sort Items by Ratio: Sort all items in descending order based on their value-to-weight ratio.

Hints: Knapsack
- Select Items Greedily:
Initialize the total value to 0 and the remaining capacity of the knapsack to W.
Iterate through the sorted list of items:
If the item's weight is less than or equal to the remaining capacity, add the entire item's value to the total value and decrease the remaining capacity accordingly.
If the item's weight exceeds the remaining capacity, take the fraction of the item that fits, add the corresponding fraction of its value to the total value, and fill the knapsack to its capacity.
Terminate When Full: Stop the process once the knapsack reaches its weight capacity or all items have been considered.Reference
Week 12: Greedy Algorithm (Lab)