Week 04: Linked Lists and Hash Tables (Lab)

Stefan-Cristian Roata

2026-02-05

Learning Objectives

By the end of this lab session, you should be able to:

  1. Develop an understanding of how stacks and queues work and implement basic algorithms using these data structures. ↪
  2. Manipulate linked lists through operations such as traversal and reversal. ↪
  3. Use hash tables to solve simple problems involving frequency counts (e.g., finding the majority element in an array). ↪

Overview of Lab Activities

Submit your work for the following activities to xSITe and/or Gradescope (as specified on each slide):

  1. Multiple-Choice Questions:

    Submit using xSITe Quiz. Total 25 marks.

  2. Implement a Queue Using 2 Stacks:

    Submit using Gradescope. Total 25 marks.

  3. Reverse a Singly-Linked List:

    Submit using Gradescope. Total 25 marks.

  4. Find the Majority Element in an Array Using a Hash Table:

    Submit using Gradescope. Total 25 marks.

Exercise 1: Multiple-Choice Questions

On the xSITe course page, navigate to Assessments → Quizzes → Week 04 Lab Exercise 1: MCQs.

Select the best answer for each of the following five questions. You may refer to your notes or the lecture slides.

Exercise 1: Question 1

Consider a singly linked list with \(n\) nodes. You are given a pointer to the head of the list, but no tail pointer.

Which of the following operations can be performed in \(\Theta(1)\) time?

  1. Insert a new node at the end of the list
  2. Delete the last node of the list
  3. Insert a new node at the beginning of the list
  4. Search for a given key in the list

Answer to Question 1

Correct Answer: c

Reasoning:

Inserting at the beginning only requires updating the head pointer. All other operations require traversing the list and therefore take \(\Theta(n)\) time.

Exercise 1: Question 2

In a singly linked list, you are given a pointer to a node \(x\) that is not the last node in the list.

Which operation can be performed in \(\Theta(1)\) time?

  1. Delete node \(x\)
  2. Delete the predecessor of \(x\)
  3. Insert a node before \(x\)
  4. Find the last node in the list

Answer to Question 2

Correct Answer: a

Reasoning:

Node \(x\) can be deleted in \(\Theta(1)\) time by copying the key and next pointer from \(x.next\) into \(x\), and bypassing the next node.

Exercise 1: Question 3

A hash table uses chaining with \(m\) slots and stores \(n\) keys. Assume simple uniform hashing, and let the load factor be \(\alpha = n / m\).

What is the average-case time for an unsuccessful search?

  1. \(\Theta(1)\)
  2. \(\Theta(\alpha \log n)\)
  3. \(\Theta (1 + \alpha)\)
  4. \(\Theta (n)\)

Answer to Question 3

Correct Answer: c

Reasoning:

Under simple uniform hashing, the expected length of each chain is \(\alpha\). An unsuccessful search must scan the entire chain in the target slot. The total time required (including computing the hash function) is \(\Theta(1 + \alpha)\).

Exercise 1: Question 4

A hash table uses chaining to resolve collisions. Each table slot stores a pointer to the head of a linked list.

Which of the following statements is always true for a hash table using chaining?

  1. The linked lists are kept in sorted order by key
  2. Each linked list contains at most \(\alpha\) keys
  3. The number of linked lists equals the number of stored keys
  4. Each key is stored in exactly one linked list

Answer to Question 4

Correct Answer: d

Reasoning:

In a hash table that uses chaining, each key is first mapped to one specific slot using the hash function. That slot contains a linked list, and the key is stored as a node in that list. Because every key is hashed once, and each key is inserted into exactly one list, a key cannot appear in more than one linked list, and it also cannot be stored outside the lists. So, each key is stored in exactly one linked list.

Why the other options are wrong:

  1. The lists are not automatically kept in sorted order; keys are usually inserted wherever convenient (often at the head).

  2. A list can be much longer than the average; the load factor is only an average, not a limit.

  3. The number of linked lists is fixed by the table size, not by how many keys are stored.

Exercise 1: Question 5

What property should a “good” hash function \(h(k)\) have when mapping keys to an \(m\)-slot hash table?

  1. Always produce prime numbers
  2. Distribute keys uniformly across slots
  3. Generate values larger than \(m\)
  4. Map similar keys to similar locations

Answer to Question 5

Correct Answer: b

Reasoning:

A good hash function should distribute keys uniformly across all available slots to minimize collisions and ensure efficient access times. Clustering keys in specific slots would degrade performance.

Stacks and Queues

Stacks

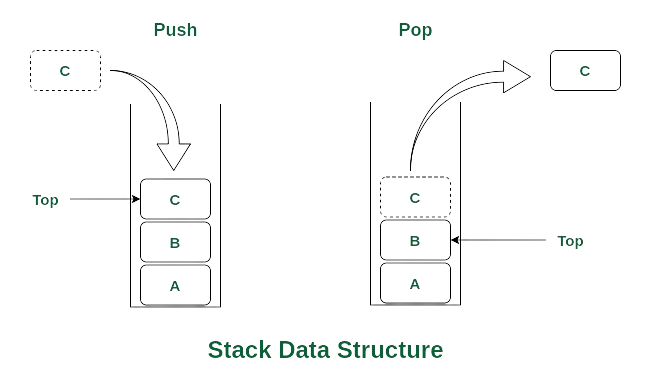
What is a Stack and How Does It Work?

A stack is a linear data structure that follows the Last In, First Out (LIFO) principle.

  • The last element added to the stack will be the first one to be removed.
  • Think of it like a stack of plates: you add new plates to the top and remove plates from the top.

Stack Basic Operations



  • Push: Add an element to the top of the stack.
  • Pop: Remove the top element from the stack.
  • Top/Peek: Retrieve the top element without removing it.
  • isEmpty: Check if the stack is empty.

Stacks Implementation in C++

Stacks can be implemented using native C++ arrays or using libraries like <stack> in the Standard Template Library (STL).

Stacks in STL (Example)

#include <iostream>
#include <stack>

int main() {
    // Declare stack
    std::stack<int> s;

    // Push elements onto stack
    s.push(10);
    s.push(20);
    s.push(30);

    // Peek at the top
    std::cout << s.top() << '\n';

    // Pop element from stack
    s.pop();

    return 0;
}

Queues

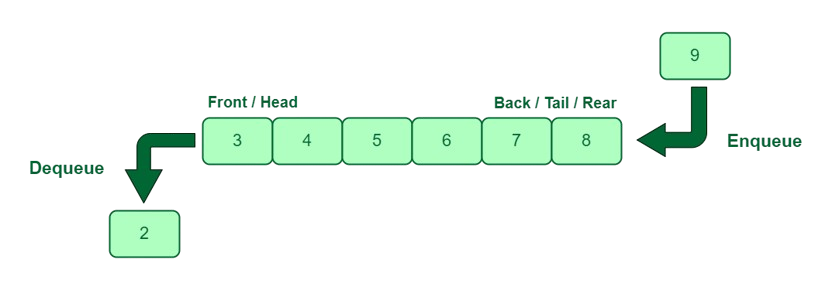
What is a Queue and How Does It Work?

A queue is a linear data structure that follows the First In, First Out (FIFO) principle.

  • The first element added to the queue will be the first one to be removed.
  • Think of it like a line of people waiting for a service: the first person in line is the first one to be served.

Queue Basic Operations



  • Enqueue: Add an element to the end of the queue.
  • Dequeue: Remove the front element from the queue.
  • Front/Peek: Retrieve the front element without removing it.
  • isEmpty: Check if the queue is empty.

Queues Implementation in C++

Queues can be implemented using native C++ arrays or using libraries like <queue> in the Standard Template Library (STL).

Queues in STL (Example)

#include <iostream>
#include <queue>

int main() {
    // Declare queue
    std::queue<int> q;

    // Enqueue elements into queue
    q.push(10);
    q.push(20);
    q.push(30);

    // Peek at the front
    std::cout << q.front() << '\n';

    // Dequeue element from queue
    q.pop();

    return 0;
}

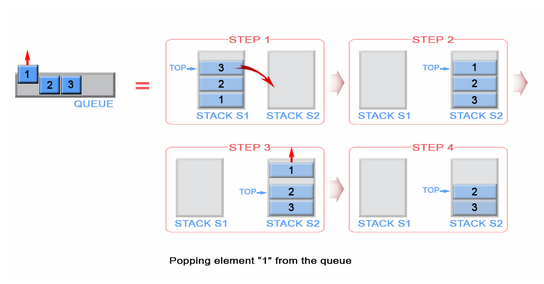
Exercise 2: Implement a Queue Using 2 Stacks

Task

Your task is to implement a queue using 2 stacks, s1 and s2.

Template

You can find the template files on xSITe (.zip archive).

Complete the partial queue_using_2_stacks.cpp file. The make command will compile the project.

Submission

Implement the .enqueue() and .dequeue() methods of the Queue struct inside queue_using_2_stacks.cpp. Do NOT use std::queue in your implementation.

To receive credit for your work, upload your completed queue_using_2_stacks.cpp file to the Gradescope assignment titled Week 04 Lab Exercise 2: Implement a Queue Using 2 Stacks.

Exercise 2: Implement a Queue Using 2 Stacks

Steps and Hints

The idea is to use the stack s1 for enqueue operations and the stack s2 for dequeue operations.

  1. For the enqueue operation, push the element onto s1.
  2. For the dequeue operation:
    • If s2 is empty, pop all elements from s1 and push them onto s2.
    • Pop the top element from s2.

Exercise 2: Visual Explanation

Here is a visual explanation of the solution:

Exercise 3: Reverse a Linked List

Task

Given the head of a singly-linked list, your task is to implement a function that reverses this linked list iteratively.

Template

You can find the template files on xSITe (.zip archive).

Complete the partial reverse_linked_list.cpp file. The make command will compile the project.

Submission

Implement the reverseList() function inside reverse_linked_list.cpp.

Do NOT use any built-in functions for reversing the list (e.g., std::reverse).

To receive credit for your work, upload your completed reverse_linked_list.cpp file to the Gradescope assignment Week 04 Lab Exercise 3: Reverse a Linked List.

Exercise 3: Reverse a Linked List

Steps and Hints

The idea is to reverse the linked list by changing the next pointers of the nodes.

  1. Initialize three pointers: prev as nullptr, current as the head of the list, and next as nullptr.
  2. Traverse the list. In each iteration:
    • Store the next node using next = current->next.
    • Reverse the current node’s pointer using current->next = prev.
    • Move the prev and current pointers one step forward using prev = current and current = next.

Hash Tables

Hash Table Implementation in C++ (Unordered Map)

One of the ways to create a hash table in C++ is to use std::unordered_map. Here is an example:

#include <iostream>
#include <unordered_map>

int main() {
    // Declare unordered_map
    std::unordered_map<std::string, int> umap;
    // Insert elements into unordered_map
    umap["apple"] = 1;
    umap["banana"] = 2;
    umap["cherry"] = 3;

    // Access elements
    std::cout << "apple: " << umap["apple"] << '\n';
    std::cout << "banana: " << umap["banana"] << '\n';

    // Check if an element exists
    if (umap.find("cherry") != umap.end()) {
        std::cout << "cherry is in the map\n";
    }

    // Remove an element
    umap.erase("banana");

    // Iterate through the unordered_map
    for (const auto& pair : umap) {
        std::cout << pair.first << ": " << pair.second << '\n';
    }
}

Exercise 4: Find the Majority Element in an Array

Task

Given an array of positive integers, your task is to implement a function that finds the majority element in this array using a hash table. An element is considered a majority element if it appears strictly more than n / 2 times in an array containing n elements.

If no majority element exists, then the function should return -1.

Examples

  1. [1, 2, 2] — element 2 is the majority element, since it appears \(2 > 3/2\) times in the array.
  2. [1, 2, 3] — no majority element exists, -1 is returned.
  3. [5, 5, 5, 8, 8, 8] — no majority element exists, -1 is returned. Both 5 and 8 appear 3 times, but either of them should appear at least \(6/2 + 1 = 4\) times to be considered the majority element.

Exercise 4: Find the Majority Element in an Array

Template

You can find the template files on xSITe (.zip archive).

Complete the partial majority_element.cpp file. The make command will compile the project.

Submission

Implement the findMajority() function inside majority_element.cpp.

Do NOT use any built-in functions for finding the majority element (e.g., std::count). You may however use std::unordered_map to instantiate your hash table.

To receive credit for your work, upload your completed majority_element.cpp file to the Gradescope assignment titled Week 04 Lab Exercise 4: Find the Majority Element.

Exercise 4: Find the Majority Element in an Array

Steps and Hints

The idea is to use a hash table to count the occurrences of each element in the array and then determine the majority element.

  1. Use an std::unordered_map to store the count of each element.
  2. Traverse the array and update the counts in the hash table. If the count of the current element already exceeds the n / 2 threshold, return this element immediately.
  3. If no element was returned previously, return -1 (no majority).